WILLナビ（ウィルナビ）─首都圏中学受験・塾・入試・学習情報サイト
協力／朝日小学生新聞・プレジデントFamily・東京出版・森上教育研究所・安田教育研究所・ワイワイネット、他
図のような１周60目盛りのタイマーがあります。細い針と太い針の２本があり，どちらも時計回りに回り続けます。細い針は60秒で１周し，太い針は細い針の$\dfrac{\text{3}}{\text{4}}$の速さで１周します。どちらの針もはじめ０を指していて，同時に動き始めるとき，次の問いに答えなさい。
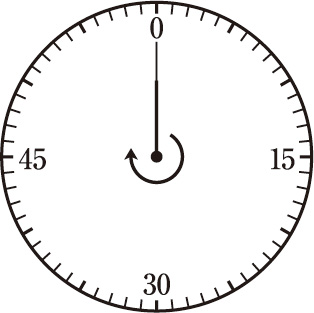
(1) 細い針が５周したとき，太い針が指している数を０から59までの整数で答えなさい。
(2) 針が動き始めてから256秒たったとき，細い針と太い針の間の角の大きさは何度ですか。ただし，180度より小さい角度を答えること。
(3) ２回目に，細い針と太い針の間の角の大きさが30度となるのは，針が動き始めてから何秒後ですか。
(1) 細い針が5周する間に，太い針は
5×$\dfrac{\text{3}}{\text{4}}$＝3$\dfrac{\text{3}}{\text{4}}$(周)します。よって，太い針が指している数は，$\dfrac{\text{3}}{\text{4}}$周に対応する
60×$\dfrac{\text{3}}{\text{4}}$＝45
(2) 1秒あたりに回る角度は，
細い針 …… 360÷60＝6(度)
太い針 …… 6×$\dfrac{\text{3}}{\text{4}}$＝4.5(度)
256秒の間に，細い針は太い針よりも
(6−4.5)×256＝384(度)
多く回ります。これは1周と24度なので，
答えは24度です。
(3) 細い針と太い針の間の角の大きさが2回目に30度となるのは，細い針が太い針よりも360−30＝330(度)多く回ったときです。よって，
330÷(6−4.5)＝220(秒後)
中学への算数
東京出版刊行
解き方のイメージを育て、思考力を鍛える！
詳しくはこちらから！
●編集方針●
最近の中学入試では、型にこだわらない新傾向問題が増えています。 これらは、ためしたり、かぞえたり、整理したり、場合を分けたり、 規則性を発見したり、グラフを書いたり、図形を動かしたり、 立体をいろいろとりあつかったり、というように、 単なる反復練習では解くことのできない、 数学的な発想力や思考力を要求される問題です。 それに応える力を育てることが本誌の最大の目標です。同時に、受験を離れたところでも、算数のおもしろさ、 楽しさを伝えていきます。
WILLナビTOPへ
WILLナビ120%活用法
トップページへ戻る
数学はRPGと同じで、いろいろな考え方や公式というスキルを習得し、それらが使えるようになって問題という敵を倒せば、どんどんレベルアップしていける教科です。ぜひ獨協で、いっしょに数学レベルを上げていきましょう！