WILLナビ（ウィルナビ）─首都圏中学受験・塾・入試・学習情報サイト
協力／朝日小学生新聞・プレジデントFamily・東京出版・森上教育研究所・安田教育研究所・ワイワイネット、他
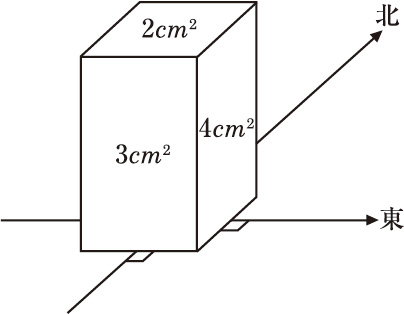
図のように，各面の面積が2cm2，3cm2，4cm2の直方体があり，この直方体の側面がちょうど東西南北になるように向いて，はじめは2cm2の面を下にして水平な台の上に置いてあります。
コインを投げて，
表が出ると北にある側面が下の面になるように直方体を1回倒し，裏が出ると東にある側面が下の面になるように直方体を1回倒します。
コインを何回か投げて，直方体を倒していき，下になった面の面積をすべて足します。例えばコインを２回投げて，表→裏の順に出たとき，北→東の順に直方体を倒すので,下になる面の面積は，3cm2，4cm2となり，下になった面の面積をすべて足すと和は7cm2です。
また，コインを２回投げて下になった面の面積をすべて足すと和が7cm2のとき，コインの出方は全部で表→裏，裏→表の２通りです。次の問いに答えなさい。
(1) コインを２回投げました。表→表の順に出たとき，下になった面の面積をすべて足すと和は何cm2ですか。
(2) コインを３回投げました。下になった面の面積をすべて足すと和が11cm2のとき，コインの出方は１通りです。その出方を答えなさい。
(3) コインを３回投げました。下になった面の面積をすべて足すと和が9cm2のとき，コインの出方は全部で何通りですか。
実際に直方体を頭の中で何度も倒すのは難しいですね。直方体を何度も倒したとき,下になる面の面積にはどのような性質があるでしょうか？
(1) 北に2回倒すので，下になった面の面積は順に3cm2，2cm2となります。よって，3＋2＝5(cm2)
(2) 2，3，4だけを使って3つの和で11を作る方法は，11＝3＋4＋4だけです。また，「下になった面の面積」で同じ面積が2回続くことはありませんから，
11＝4＋3＋4の順番に決まります。そのとき，コインの出方は裏→表→表です。
(3) 2，3，4だけを使って3つの和で9を作る方法は，9＝2＋3＋4＝3＋3＋3です。このうち，3＋3＋3は同じ面積が続くので不適です。2＋3＋4については，1回目に下になる面の面積が3cm2か4cm2のどちらかでありさえすれば，すべての順番が起こりえます。
よって，2×2×1＝4(通り)
中学への算数
東京出版刊行
解き方のイメージを育て、思考力を鍛える！
詳しくはこちらから！
●編集方針●
最近の中学入試では、型にこだわらない新傾向問題が増えています。 これらは、ためしたり、かぞえたり、整理したり、場合を分けたり、 規則性を発見したり、グラフを書いたり、図形を動かしたり、 立体をいろいろとりあつかったり、というように、 単なる反復練習では解くことのできない、 数学的な発想力や思考力を要求される問題です。 それに応える力を育てることが本誌の最大の目標です。同時に、受験を離れたところでも、算数のおもしろさ、 楽しさを伝えていきます。
WILLナビTOPへ
WILLナビ120%活用法
トップページへ戻る
本校では計算力と思考力を育むことを目標にして、成長段階に応じた取り組みを行っています。
中学では基礎的な計算力を身に付けられるように、計算力診断テストを繰り返し実施し、図形の証明などで発想力・表現力を磨いています。中３からは高校の内容を先取りし、各単元を通じて思考力も養っていきます。
様々な角度から条件を眺め、上手に組み合わせることによって問題を解きほぐしていく。数学の問題を解きながら、論理的思考を身に付けて欲しいと考えています。