WILLナビ（ウィルナビ）─首都圏中学受験・塾・入試・学習情報サイト
協力／朝日小学生新聞・プレジデントFamily・東京出版・森上教育研究所・安田教育研究所・ワイワイネット、他
下の図は，１辺が18cmの立方体です。点Pは辺AE上を毎秒1cmで，点Aから点Eまで移動します。また，点Qは辺CG上にありCQ＝12cm，点Rは辺EF上にありER=4.5cmとなる点です。
次の各問いに答えなさい。
ただし，角すいの体積は（底面積）×（高さ）× $\dfrac{\text{1}}{\text{3}}$ で求めることができます。
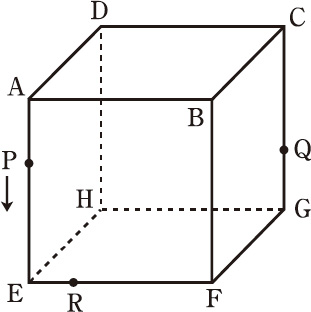
(1) 点Pが点Aを出発してから６秒後に，この立方体を，3点D，P，Qを通る平面で切断しました。点Hを含む立体の体積は何cm3ですか。
(2) 点Pが点Aを出発してから12秒後に，この立方体を，3点D，P，Qを通る平面で切断しました。点Hを含む立体の体積は何cm3ですか。
(3) 点Pが点Aを出発してから15秒後に，この立方体を，3点D，P，Rを通る平面で切断しました。点Hを含む立体の体積は何cm3ですか。
(1) AP＝6cmです。Pを通りABと平行な直線と辺BFの交点をSとし，Pを通りDQと平行な直線と辺BFまたはその延長との交点をTとします。三角形PSTは三角形DCQと合同で，
BT＝BS＋ST＝AP＋CQ＝6＋12＝18(cm)
となるので，TはFと重なります。
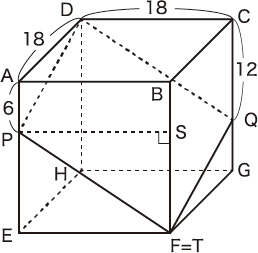
結局，もとの立方体が合同な2つの立体に分かれるので，求める体積は，
18×18×18÷2＝2916(cm3)
(2) AP＝12cmです。(1)と同じようにTをとると，BT＝12＋12＝24(cm)です。
すると，次の図でFT，PE，QGの長さがすべて6cmとなり，三角形FTUと三角形EPUの合同からFU＝18÷2＝9(cm)で，FVの長さも同様に9cmです。
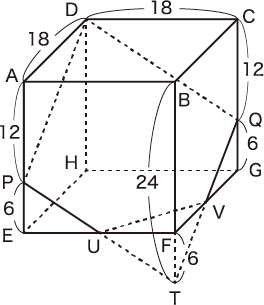
よって，点Bを含む立体の体積は，
18×18×24÷2−9×9÷2×6÷3＝18×18×12−81(cm3)
点Hを含む立体の体積は，
18×18×18−(18×18×12−81)＝18×18×(18−12)＋81
＝2025(cm3)
(3) AP＝15cmです。Dを通りPRと平行な直線を引き，辺CGとの交点をWとします。三角形PERと三角形WCDは相似で，PE：ER＝3：4.5＝2：3なので，
CW＝18×$\dfrac{\text{2}}{\text{3}}$＝12(cm)です。よって，WはQと重なり，3点D，P，Qを通る平面による切断と同じことです。
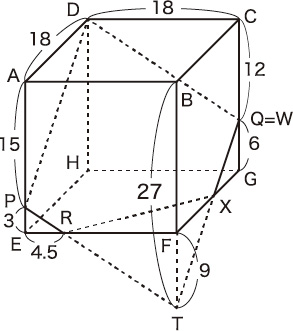
(1)と同じようにTをとると，BT＝15＋12＝27(cm)です。
図で，FR＝18−4.5＝13.5(cm)です。
また，三角形FTXと三角形GQXは相似で，相似比は9：6＝3：2ですから，
FX＝18×$\dfrac{\text{3}}{\text{3+2}}$＝10.8(cm)
よって，点Bを含む立体の体積は，18×18×27÷2−13.5×10.8÷2×9÷3＝18×18×13.5−218.7(cm3)
点Hを含む立体の体積は，
18×18×18−(18×18×13.5−218.7)＝18×18×(18−13.5)＋218.7
＝1676.7(cm3)
中学への算数
東京出版刊行
解き方のイメージを育て、思考力を鍛える！
詳しくはこちらから！
●編集方針●
最近の中学入試では、型にこだわらない新傾向問題が増えています。 これらは、ためしたり、かぞえたり、整理したり、場合を分けたり、 規則性を発見したり、グラフを書いたり、図形を動かしたり、 立体をいろいろとりあつかったり、というように、 単なる反復練習では解くことのできない、 数学的な発想力や思考力を要求される問題です。 それに応える力を育てることが本誌の最大の目標です。同時に、受験を離れたところでも、算数のおもしろさ、 楽しさを伝えていきます。
WILLナビTOPへ
WILLナビ120%活用法
トップページへ戻る
高校課程では習熟度別授業やコース分けが導入されていますので、問題を解ける喜びや数学の楽しさを味わえる環境が整っています。授業ではただ板書をノートに写すのではなく、自分で考えて正解を導く努力をして下さい。そうすれば大学生や社会人になったとき、数学を1つの手段として用いることができるようになり、更には数学そのものの魅力に気づくはずです。