WILL�i�r�i�E�B���i�r�j����s�����w�E�m�E�����E�w�K���T�C�g
���́^�������w���V���E�v���W�f���gFamily�E�����o�ŁE�X�㋳�猤�����E���c���猤�����E���C���C�l�b�g�A��
WILL�i�r�i�E�B���i�r�j����s�����w�E�m�E�����E�w�K���T�C�g
���́^�������w���V���E�v���W�f���gFamily�E�����o�ŁE�X�㋳�猤�����E���c���猤�����E���C���C�l�b�g�A��



 (3) �E�̐}�̂悤�Ȑ����`�̃^�C������ׂĖ͗l������܂��B
(3) �E�̐}�̂悤�Ȑ����`�̃^�C������ׂĖ͗l������܂��B
���̌`�ɕ��ׂ�Ƃ��C���ʂ�̖͗l���l�����܂����B�������C�^�C���͉�]���Ďg���Ă��悢�ł����C���ʂ͎g���܂���B�܂��C��]���ē����͗l�ɂȂ���̂͂P�̖͗l�Ƃ݂Ȃ��܂��B
�@�@�ȉ���A�`F��6�ʂ��ł��B

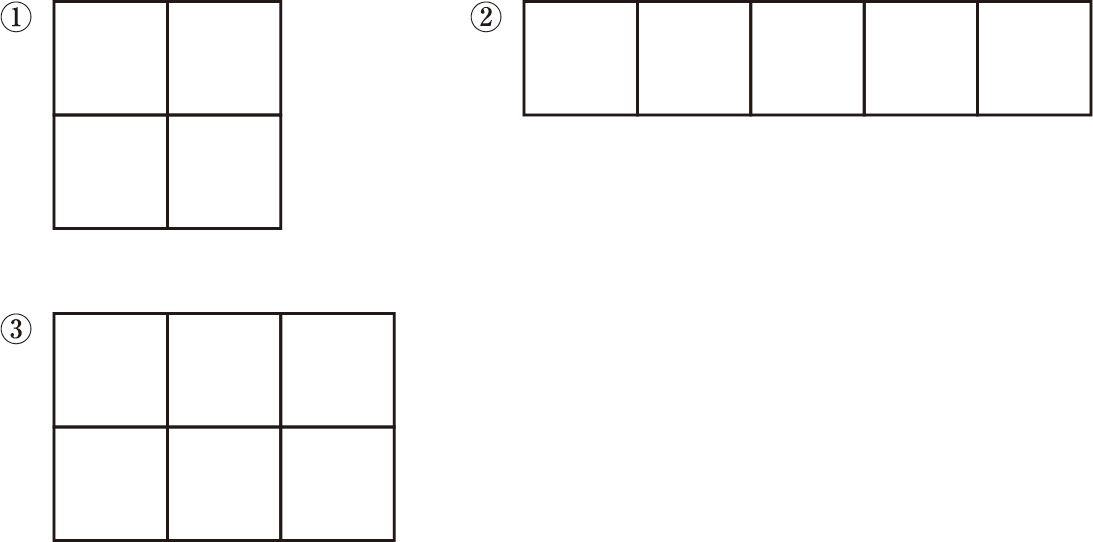
�A�@���̐}�̂悤�ɁC5���̃^�C���ɇ@�`�D�̔ԍ������܂��B

��]���ē����͗l�ɂȂ���̂����ׂċ�ʂ���ƁC�͗l��
2×2×2×2×2��32(�ʂ�) …… �i�A�j
����܂��B
���̂����C180�x��]���Ď������g�Əd�Ȃ�͗l�́C�@�ƇD�������ŁC�A�ƇC���������̂ł��B�@�`�B�̃^�C�������߂�ƍl���āC
2×2×2��8(�ʂ�)
�i�A�j�̂����C����8�ʂ�ȊO�̖͗l�́C180�x��]���邱�Ƃ�2���g�ɂȂ�܂��B
����āC
(32�|8)÷2�{8��20(�ʂ�)
�B�@���̐}�̂悤�ɁC6���̃^�C���ɇ@�`�E�̔ԍ������܂��B
��]���ē����͗l�ɂȂ���̂����ׂċ�ʂ���ƁC�͗l��
2×2×2×2×2×2��64(�ʂ�) …… �i�C�j
����܂��B
���̂����C180�x��]���Ď������g�Əd�Ȃ�͗l�́C�@�ƇE�������ŁC�A�ƇD�������ŁC�B�ƇC���������̂ł��B�@�`�B�̃^�C�������߂�ƍl���āC
2×2×2��8(�ʂ�)
�i�C�j�̂����C����8�ʂ�ȊO�̖͗l�́C180�x��]���邱�Ƃ�2���g�ɂȂ�܂��B
����āC
(64�|8)÷2�{8��36(�ʂ�)
���w�ւ̎Z��
�����o�Ŋ��s
�������̃C���[�W����āA�v�l�͂�b����I

 �ڂ����͂����炩��I
�ڂ����͂����炩��I
���ҏW���j��
�ŋ߂̒��w�����ł́A�^�ɂ������Ȃ��V�X����肪�����Ă��܂��B �����́A���߂�����A����������A����������A�ꍇ������A �K������������A�O���t����������A�}�`��������A ���̂����낢��Ƃ肠��������A�Ƃ����悤�ɁA �P�Ȃ锽�����K�ł͉������Ƃ̂ł��Ȃ��A ���w�I�Ȕ��z�͂�v�l�͂�v���������ł��B ����ɉ�����͂���Ă邱�Ƃ��{���̍ő�̖ڕW�ł��B�����ɁA�𗣂ꂽ�Ƃ���ł��A�Z���̂������낳�A �y������`���Ă����܂��B
�@�_���I�v�l�ɂ��������\�͂��s���Ȍ���Љ�ɂ����Ă͊�]�i�H�ɂ�����炸�A���w���w�ԕK�v������܂��B�����ŁA�ǂ̐��k�������Ȃ��w�K��i�߂���悤�ɁA�����w�N�ŃN���X�����鏭�l�����Ƃ����{���A�܂��A���e�X�g��i�x�ɍ��킹�ēK�X�i���Q�̉��K���Ƃł͖���j�s���e���̗���x���m���߂�Ȃǂ̍H�v�����Ă��܂��B